Abstract
Shear wave velocity (Vs) is a key parameter in geotechnical engineering, yet its prediction is often challenged by the scarcity and heterogeneity of available datasets. This study proposes a clustering-based local modeling framework to enhance Vs prediction performance in small-data scenarios. The approach begins by extending the original challenge dataset with additional sources and generating augmented samples through controlled perturbations of independent input variables, followed by recalculation of derived dependent parameters while keeping Vs fixed. After normalizing features, clustering techniques are applied to identify data structure in local regions of data and eliminate outliers, improving the reliability of the training set. Local predictive models are then trained within each cluster using Multi-Layer Perceptron (MLP) and Random Forest (RF), enabling a comparative assessment of deep learning and ensemble-based approaches. Results show that combining data augmentation, clustering, and local model training substantially improves predictive performance and robustness compared to global models on raw data. The findings underline the potential of clustering-based local deep and ensemble models for shear wave velocity prediction in small datasets, offering practical value for machine learning applications in geotechnical engineering.
Data Preperation
Data Augmentation
The original dataset provided in the AI Vs. 2025 challenge is relatively small, which posed a risk of overfitting and limited the generalization ability of predictive models. To overcome this, a systematic data augmentation strategy is implemented. Two external datasets containing similar geotechnical features from a real case in New Zealand are integrated with the original challenge dataset, increasing both the size and diversity of the training pool. In addition, synthetic samples are generated by applying controlled perturbations to selected input variables (qt, fs, z, u2). These parameters are varied randomly by ±0.5%, ±1.0%, ±0.2%, and ±1.0%, simulating realistic measurement noise and natural variability. For each perturbed sample, the dependent indices (Qt, Bq, Ic, Fr) are recalculated using domain-specific formulas, while the target parameter (Vs) is preserved. This ensured that the augmented data retained physical consistency and meaningful correlations with the target variable
The distribution of original data is shown in Fig. 1(a), for the concatenated external data in Fig. 1(b) and for the augmented data is shown in Fig. 1(c). It is clear that more data are available around each test data in each cluster allowing a better prediction and generalization as the results imply in the next section.
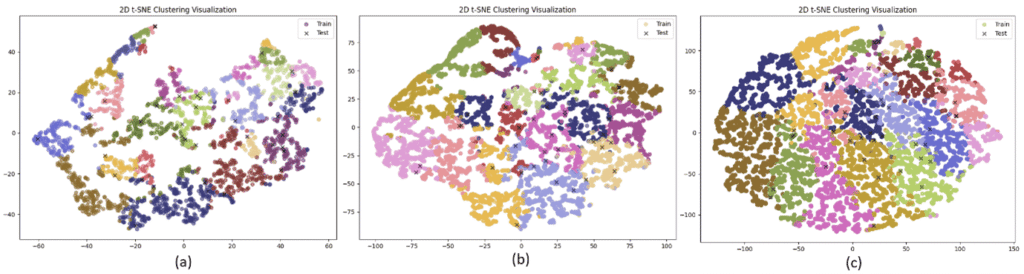
Figure 1: Distribution of data using TSNE, (a) original data, (b) concatenated data, (c) augmented data.
Preprocessing and Feature Selection
We have tested different combinations of (z, qt, fs, u2, Qt, Fr, Bq, Ic) as features during ablation study and found out that the best combination is to use all eight features. Generally, MLP methods can model nonlinear systems properly even with high dimension features while for RF method this is not a big deal as far as we have enough data for training purposes. The features are then normalized based on the Min and Max values to make it suitable for deep models.
Clustering and Outlier Removal
The preprocessed data were grouped into 20 clusters using K-means, and samples far from cluster centers were removed as outliers. Clustering enables localized models instead of a single global one, improving prediction since shear wave velocity data often comes from diverse applications with varying sensors. By grouping similar samples, clustering reduces heterogeneity and trains models on more consistent subsets, leading to more robust predictions. Outlier removal further eliminates noise from excessive augmentation, enhancing accuracy. The choice of 20 clusters was based on an ablation study across different cluster numbers.
Clustering-based Local MLP and RF
For the shear wave velocity prediction task, two complementary machine learning models are employed: Random Forest and Multi-Layer Perceptron. RF, as a tree-based ensemble method, provides robustness against noise and performs well in small datasets by averaging over multiple decision trees, reducing variance and overfitting. In contrast, MLP, as a deep learning model, offers greater flexibility to capture complex nonlinear relationships in the augmented and clustered data but generally require larger datasets and careful tuning to avoid overfitting. Experimental results show that RF achieved more stable performance across clusters, while MLP outperformed RF when sufficient high-quality samples are available, highlighting a trade-off between stability and flexibility in small-sample shear wave velocity prediction.
Results
The MSE errors of RF and MLP methods applied to original data, concatenated of extra and original data, and the augmented data are shown in Tab.1. It is clear that MLP model has better results as it can fit the data better while RF achieved more stable results. Moreover, the best results of both models are on the augmented data. Fig.2 presents the MSE error of RF and MLP methods based on different number of clusters allowing us to select the best number of clusters for our method.
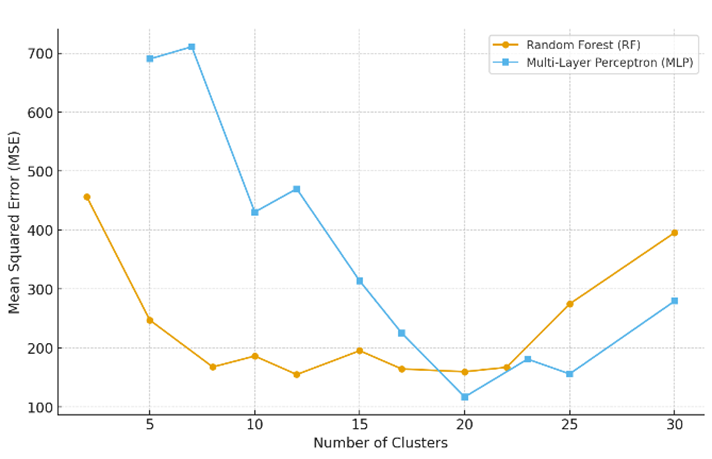
Figure 2: MSE vs number of clusters in RF and MLP methods.

Table 1. MSE of predicting Vs on our original/concatenated/augmented data using RF and MLP methods.
